Data Setting

Population: \(Y \sim\) something with c.d.f \(F_Y(y) = P(Y \le y)\)

Parameter: \(M = F^{-1}_Y(0.5)\), the population median

Sample: \(n\) i.i.d from population: \(Y_1, \ldots, Y_n\)

Null hypothesis: \(H_0: M = M_0\)

Your Turn:

Consider the hypothesis \(H_0: M = M_0\)

Imagine transforming the \(Y_i, \, i = 1, \ldots, n\) to \[ X_i = \begin{cases} 1, & Y_i \le M_0 \\ 0, & Y_i > M_0 \end{cases} \]

If the null hypothesis is true \(M = M_0\), what is \(P(X_i = 1)\)?

(You can assume \(Y\) is a continuous distribution)

Sign test

To test \(H_0: M = M_0\), perform a Binomial test on \(X_i = \pmb{1}\{Y_i \le M_0 \}\) with \(H_0: p = 0.5\).

Example

Consider a sample, \(n = 12\), with the sample values:

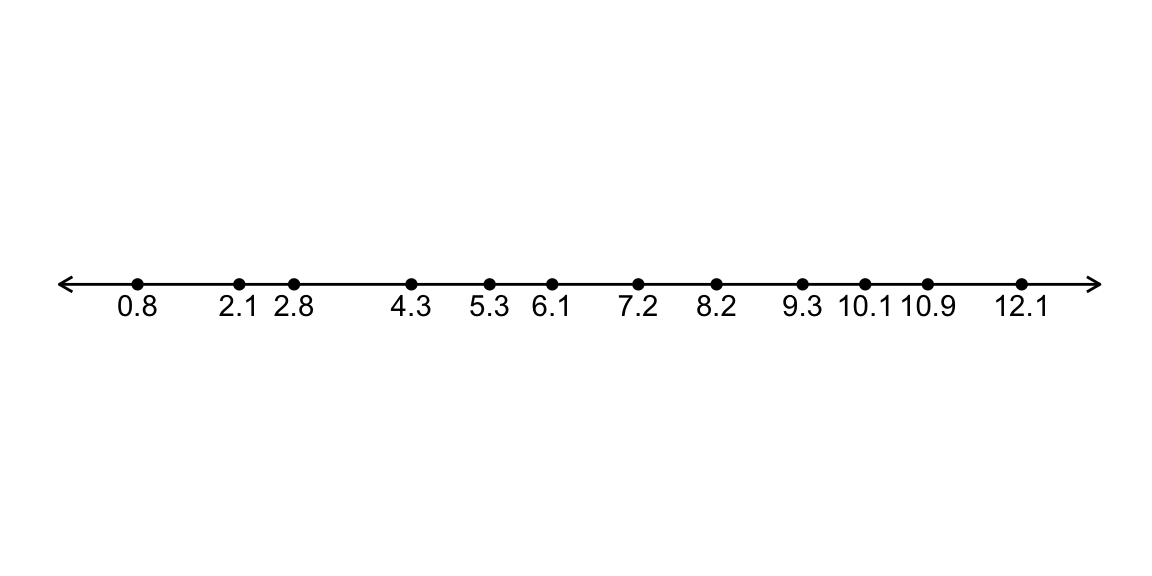
Consider testing \(H_0: M = 4\) versus a two-sided alternative \(H_A: M \ne 4\) (at the \(\alpha = 0.05\) level).

\(X_i = \pmb{1}\{Y_i \le 4 \}\)

\(\hat{p}_{M_0} = \frac{1}{n}\sum_{i = 1}^{n}X_i = 0.25\)

\(Z(p_0 = 0.5) = \frac{\hat{p}_{M_0} - p_0}{\sqrt{p_0(1-p_0)/n}} = -1.73\)

Compare to \(z_{1-\alpha/2} = 1.96\)

We fail to reject the null hypothesis.

Your turn: 95% Confidence Interval

We can invert the test by considering all \(M_0\) for which we would fail to reject the null hypothesis \(H_0: M = M_0\).

Would you reject for the value on your slip of paper?

Why do we only need to consider the actual sample values?

Your turn: 95% Confidence Interval

##     m_0
## 1   0.8
## 2   2.1
## 3   2.8
## 4   4.3
## 5   5.3
## 6   6.1
## 7   7.2
## 8   8.2
## 9   9.3
## 10 10.1
## 11 10.9
## 12 12.1

95% confidence interval for \(M\) is \((\qquad, \qquad)\)

Confidence interval in general

Solve for \(M_0\) that satisfy (i.e. not in rejection region)

\[ \left| \frac{X/n - 0.5}{0.5 \sqrt{n}} \right| < z_{1-\alpha/2}, \quad \text{where } X = \text{number of observations } \le M_0 \]

\[ -z_{1-\alpha/2} < \frac{X/n - 0.5}{0.5 / \sqrt{n}} < z_{1-\alpha/2} \]

\[ \begin{aligned} n(0.5 -z_{1-\alpha/2}\frac{0.5}{\sqrt{n}}) &< X < n(0.5 + z_{1-\alpha/2}\frac{0.5}{\sqrt{n}}) \\ \frac{1}{2}(n -z_{1-\alpha/2}\sqrt{n}) &< X < \frac{1}{2}(n + z_{1-\alpha/2}\sqrt{n}) \end{aligned} \]

Confidence interval in general

So, \(M_0\) is in interval if the number of observations smaller than \(M_0\) is between: \[ \frac{1}{2}(n -z_{1-\alpha/2}\sqrt{n}) \quad \text{ and } \quad \frac{1}{2}(n + z_{1-\alpha/2}\sqrt{n}) \]

The smallest value that satisifies this is the \[ \left(\frac{1}{2}(n -z_{1-\alpha/2}\sqrt{n})\right)^{\text{th}} \text{ smallest observation} \]

The largest value that satisifies this is the \[ \left(\frac{1}{2}(n + z_{1-\alpha/2}\sqrt{n}) + 1\right)^{\text{th}} \text{ smallest observation} \]

Confidence interval for median

Approximate (based on approximate Binomial test) confidence interval for the median:

\[ \begin{aligned} \Biggl( \left(\frac{n - z_{1-\alpha/2}\sqrt{n}}{2} \right)^{\text{th}} \text{ smallest observation}, \\ \left(\frac{n + z_{1-\alpha/2}\sqrt{n}}{2} + 1 \right)^{\text{th}} \text{ smallest observation}\Biggr) \end{aligned} \]

May need to round \((.)^\text{th}\) to nearest integers

Example, continued

\(n = 12, \alpha = 0.05 \implies\)

\[ \begin{aligned} &\Biggl(\left(\frac{12 - 1.96\sqrt{12}}{2} \right)^{\text{th}} \text{ smallest observation}, \\ &\qquad \left(\frac{12 +1.96\sqrt{12}}{2} + 1 \right)^{\text{th}} \text{ smallest observation} \Biggr) \\ &\left(\left(2.61\right)^{\text{th}} \text{ smallest observation}, \left(10.40\right)^{\text{th}} \text{ smallest observation} \right)\\ &\left(3^{\text{rd}} \text{ smallest observation}, 10^{\text{th}} \text{ smallest observation} \right) \\ &\left(2.8, 10.1 \right) \end{aligned} \]

Sign test for discrete distributions/data

1. Remove all values exactly equal to \(M_0\)
2. Proceed with test as usual (with a reduced sample size \(n\))

Sign test: exactness

Finite sample exact? No

• Discrete nature of data means we can’t achieve a lot of signficance levels
• Normal approximation is only an approximation…

Assymptotically exact? Yes

Sign test: consistency

The sign test test is consistent. Comes from Binomial test being consistent (which comes from Z-test being consistent).

Next time…

Signed Rank test