Tests of center

Two tests of scale

1. Chi-square test of variance

2. t-test of variance

Chi-square test of variance

Population: $Y\sim$ some population distribution

Sample: n i.i.d from population, $Y_1,\dots ,Y_n$

Parameter: Population variance ${\sigma }^2=Var\left(Y\right)$

Sample variance

The sample variance, $$s^2=\frac{1}{n-1}\sum _{i=1}^n{\left(Y_i-\overline{Y}\right)}^2$$

is an unbiased and consistent estimate of ${\sigma }^2$.

Furthermore, if $Y\sim N(\mu ,\sigma )$, it can be shown the sampling distribution of $s^2$ is a scaled Chi-square distribution: $$(n-1)\frac{s^2}{{\sigma }^2}\sim {\chi }_{(n-1)}^2$$

Using the sampling distribution to formulate a test

Assume the population distribution is $N(\mu ,{\sigma }^2)$.

Consider the null hypothesis $H_0:{\sigma }^2={\sigma }_0^2$.

Let the test statistic be: $$X\left({\sigma }_0^2\right)=(n-1)\frac{s^2}{{\sigma }_0^2}$$ What’s the distribution of the test statistic if the null hypothesis is true?

Rejection regions

For a test at level $\alpha$:

• $H_A:{\sigma }^2>{\sigma }_0^2$: Reject $H_0$ if $X\left({\sigma }_0^2\right)>$
• $H_A:{\sigma }^2<{\sigma }_0^2$: Reject $H_0$ if $X\left({\sigma }_0^2\right)<$
• $H_A:{\sigma }^2\ne {\sigma }_0^2$: Reject $H_0$ if $X\left({\sigma }_0^2\right)>$
  or $X\left({\sigma }_0^2\right)<$

p-values: Your turn

Shade the area for the p-value when $X\left({\sigma }_0\right)=20$, with $H_A:{\sigma }^2>{\sigma }_0^2$

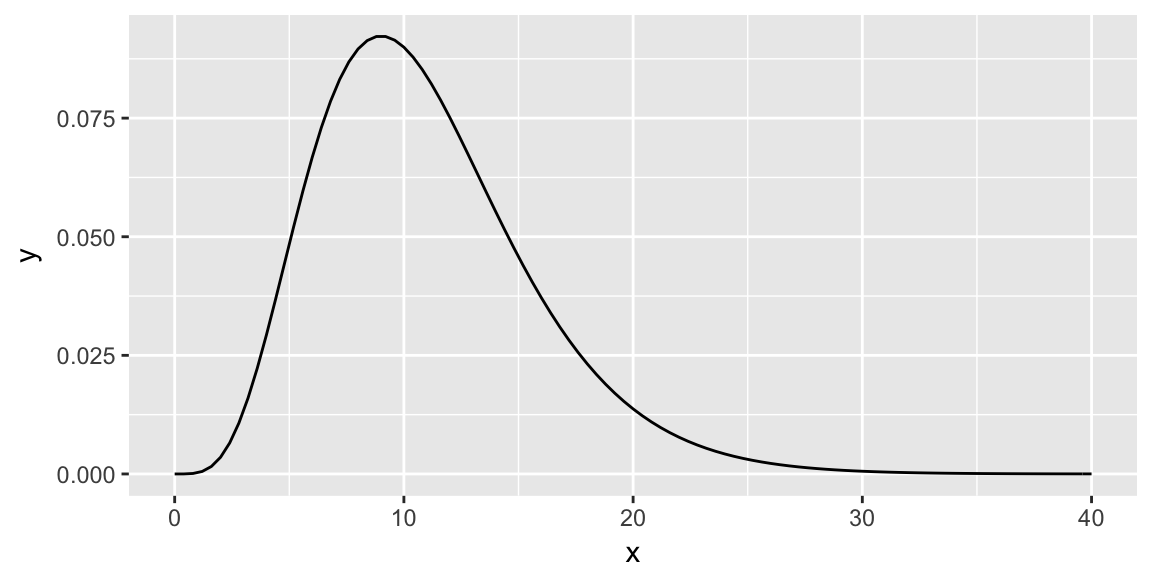
Shade the area for the p-value when $X\left({\sigma }_0\right)=20$, with $H_A:{\sigma }^2<{\sigma }_0^2$

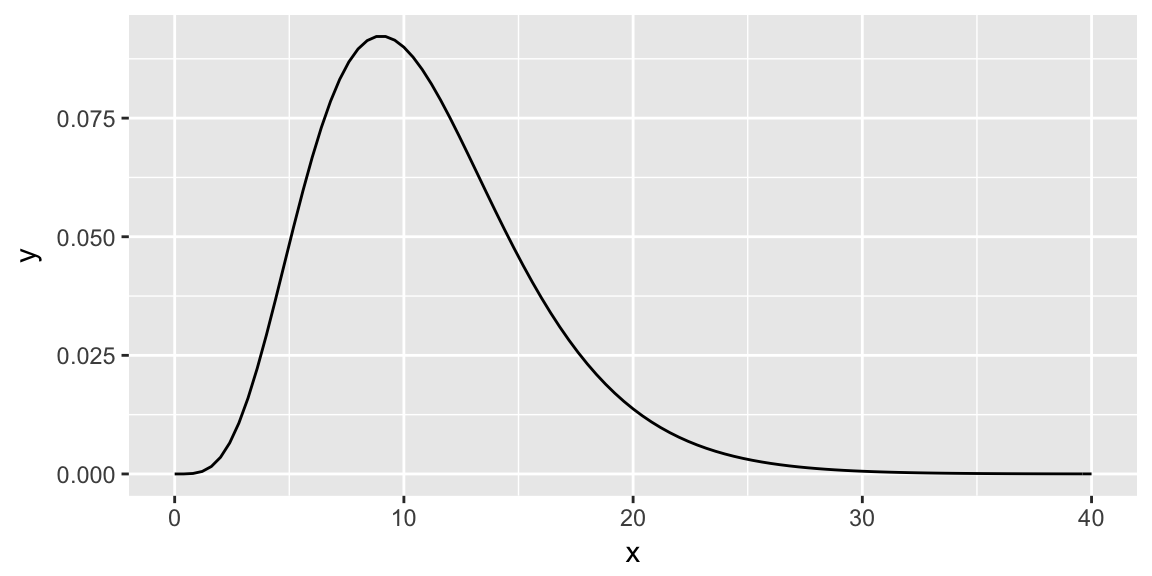
p-values: Your turn

Shade the area for the p-value when $X\left({\sigma }_0\right)=20$, with $H_A:{\sigma }^2\ne {\sigma }_0^2$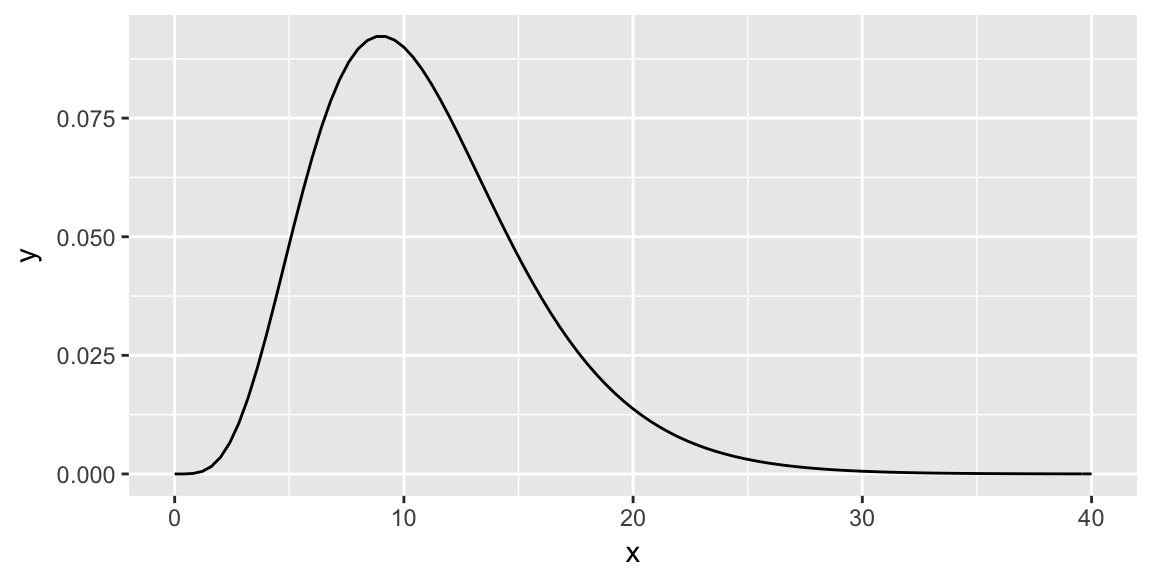

p-values: In general

p-value is:

• $H_A:{\sigma }^2>{\sigma }_0^2$:
• $H_A:{\sigma }^2<{\sigma }_0^2$:
• $H_A:{\sigma }^2\ne {\sigma }_0^2$:

where $X\sim {\chi }_{(n-1)}^2$

In R: $P(X\le x)$ = pchisq(x, df = n - 1)

Confidence interval

From inverting test statistic.

$(1-\alpha )100$% confidence interval

$$\left(\frac{s^2(n-1)}{{\chi }_{(n-1)}^2(1-\alpha /2)},\frac{s^2(n-1)}{{\chi }_{(n-1)}^2\left(\alpha /2\right)}\right)$$

What if the population isn’t Normal

(from Sarah Emerson’s slides F2016)

t-test of variance

An alternative to the Chi-square test of variance, based on considering a transformed response:

$$Z_i={\left(Y_i-\overline{Y}\right)}^{2}i=1,\dots ,n$$

What is $E\left(Z\right)$, are the $Z_i$ independent?

A CLT for the sample variance

The $Z_i$ aren’t independent but are weakly dependent, turns out there is a CLT for this case, as long as $Z$ has finite fourth moment:

$$\frac{\overline{Z}-E\left(Z\right)}{\sqrt{Var\left(Z\right)/n}}{\to }_{d}N(0,1)$$

Substitute in for $E\left(Z\right)$ $$\frac{\overline{Z}-\frac{n-1}{n}{\sigma }^2}{\sqrt{Var\left(Z\right)/n}}{\to }_{d}N(0,1)$$

Leads to a t-test

We don’t know the population variance of the $Z$ (transformed $Y$), so substitute sample estimate for it.

Under null hypothesis $H_0:{\sigma }^2={\sigma }_0^2$

$$t\left({\sigma }_0^2\right)=\frac{\overline{Z}-\frac{n-1}{n}{\sigma }_0^2}{\sqrt{s_Z^2/n}}\dot{\sim }{t}_{(n-1)}$$

So to test the null $H_0:{\sigma }^2={\sigma }_0^2$, do a t-test on $Z_i={\left(Y_i-\overline{Y}\right)}^2$ with the null hypothesis $H_0:{\mu }_Z=\frac{n-1}{n}{\sigma }_0^2$.

Performance of t-test of variance

Charlotte’s simulations, rejection rate of $H_0$ for $\alpha =0.05$.