Delta Method

If the sampling distribution of a statistic converges to a Normal distribution, the Delta method, provides a way to approximate the sampling distribution of a function of a statistic.

Univariate Delta Method

If \[ \sqrt{n}\left(\hat{\theta} - \theta \right) \rightarrow_D N(0, \sigma^2) \]

then \[ \sqrt{n}\left(g(\hat{\theta}) - g(\theta) \right) \rightarrow_D N(0, \sigma^2[g'( \theta]^2 ) \]

(As long as \(g'(\theta)\) exists and is non-zero valued.)

Another way of saying it

If we know, \[ \hat{\theta} \, \dot \sim \, N(\theta, \sigma^2) \]

then,

\[ g(\hat{\theta}) \, \dot \sim \, N(g(\theta), \sigma^2[g'(\theta)]^2) \]

The approximation can be pretty rough. I.e. just because the sample is large enough that the original statistic is reasonably Normal, doesn’t meant the transformed statistic will be.

Example: Log Odds

Let \(Y_1, \ldots, Y_n \sim\) Bernoulli\((p)\), and \(X = \sum_{i=1}^n Y_i\).

We know \(\hat{p} = \frac{X}{n} \sim N(p, \frac{p(1 - p)}{n})\).

We might estimate the log odds with: \[ \log\left(\frac{\hat{p}}{1-\hat{p}}\right) \]

What is the assymptotic distribution of the estimated log odds?

Example: Log Odds cont.

\[ g(p) = \log\left(\frac{p}{1-p}\right) = \log(p) - \log{(1-p)} \]

Other comments on delta method

Derived using a Taylor expansion of \(g(\hat{\theta})\) around \(g(\theta)\)

There is also a multivariate version (useful if you need some function of two statistics, e.g. ratio of sample means)

Bootstrap

A method to approximate the sampling distribution of a statistic

Idea:

• Recall, one way to approximate the sampling distribution of a statistic was by simulation, but you have to assume a population distribution.
• The bootstrap uses the empirical distribution function as an estimate for the population distribution, i.e relies on \[ \hat{F}(y) \approx F(y) \]

Example - Sampling distribution of Median by simulation

Assume a population distribution, i.e. \(Y \sim N(\mu, \sigma^2)\)

Repeat for \(k = 1, \ldots, B\)

1. Sample \(n\) observations from \(N(\mu, \sigma^2)\)
2. Find sample median, \(m^{(k)}\)

Then the simulated sample medians, \(m^{(k)}, k = 1, \ldots, B\) approximate the sampling distribution of the sample median.

Example - Sampling distribution of Median by bootstrap

Estimate the population distribution from the sample, i.e. \(\hat{F}(y)\)

Repeat for \(k = 1, \ldots, B\)

1. Sample \(n\) observations from a population with c.d.f \(\hat{F}(y)\)
2. Find sample median, \(m^{(k)}\)

Then the bootstrapped sample medians, \(m^{(k)}, k = 1, \ldots, B\) approximate the sampling distribution of the sample median.

Sampling from a c.d.f

You can sample from any c.d.f by sampling from a Uniform(0, 1), then transforming with the inverse c.d.f.

I.e. sample \(u_1, \ldots, u_n\) i.i.d from Uniform(0,1), then

\[ y_i = F^{-1}(u_i) \quad i = 1, \ldots, n \] are distributed with c.d.f \(F(y)\).

In the empirical case

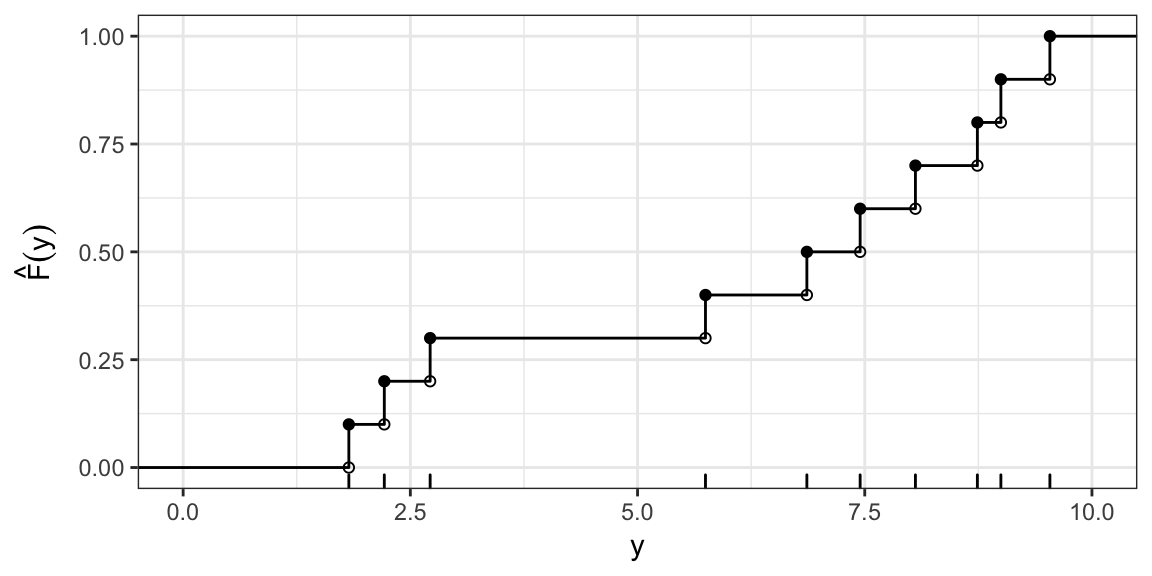
Sampling from the ECDF is equivalent to sampling with replacement from the original sample.

Example - Sampling distribution of Median by bootstrap

Repeat for \(k = 1, \ldots, B\)

1. Sample \(n\) observations with replacement from \(Y_1, \ldots, Y_n\)
2. Find sample median, \(m^{(k)}\)

Then the bootstrapped sample medians, \(m^{(k)}, k = 1, \ldots, B\) approximate the sampling distribution of the sample median.

A little more subtly: \[ \hat{m} - m \, \dot \sim \, \tilde{m} - \hat{m} \]

Example

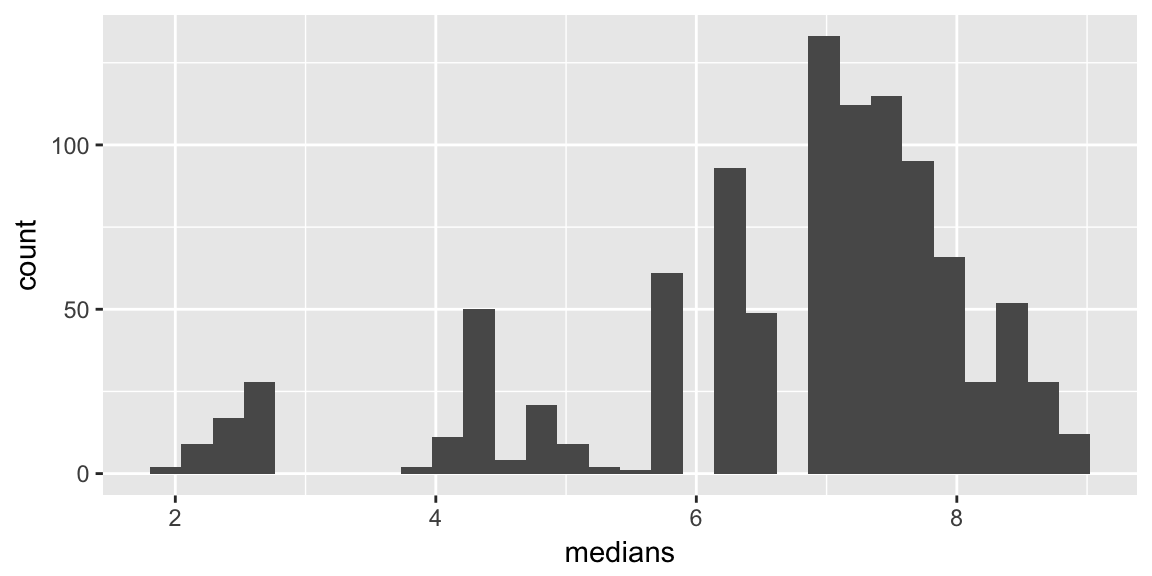
Sample values: 1.8, 2.2, 2.7, 5.7, 6.9, 7.4, 8.1, 8.7, 9 and 9.5

Sample median: 7.1562828

A bootstrap resample: 1.8, 2.7, 2.7, 5.7, 6.9, 7.4, 8.1, 8.1, 8.7 and 9.5

Sample median: 7.1562828

Many resamples

Bootstrap confidence intervals

Many methods..

A common one:

• Quantile: \(100(\alpha/2)\) largest resampled statistic value, and \(100(1 - \alpha/2)\) largest resampled statistic value

Comments on the bootstrap

Relies on \(\hat{F}(y)\) being a good estimate of the \(F(y)\), doesn’t necessarily solve small sample problems.

Resampling should generally mimic original study design. E.g. If pairs of observations are sampled from a population, pairs should be resampled