Randomization/Permutation tests ST551 Lecture 28

Announcements

I haven’t received any suggestions for the formula sheet…draft on class webpage

Homeworks:

  • 40% of your grade
  • Lowest (%) HW dropped
  • Remaining 8 homeworks will be weighted equally (i.e. 5% each)
  • I’ll update canvas with this contribution after HW #8 graded

Friday: no lecture, I’ll be in my office.

Randomized experiments

Two common study designs

  1. Random Sampling study

    • A population(s) is defined

    • Units are randomly sampled from the population(s)

    • Units are observed

  2. Randomized Experiment

    • A group of units is selected

    • Units are randomly assigned to different levels of a treatment variable

    • Units are observed

Random Sampling Model

Randomized Experiment Model

Example

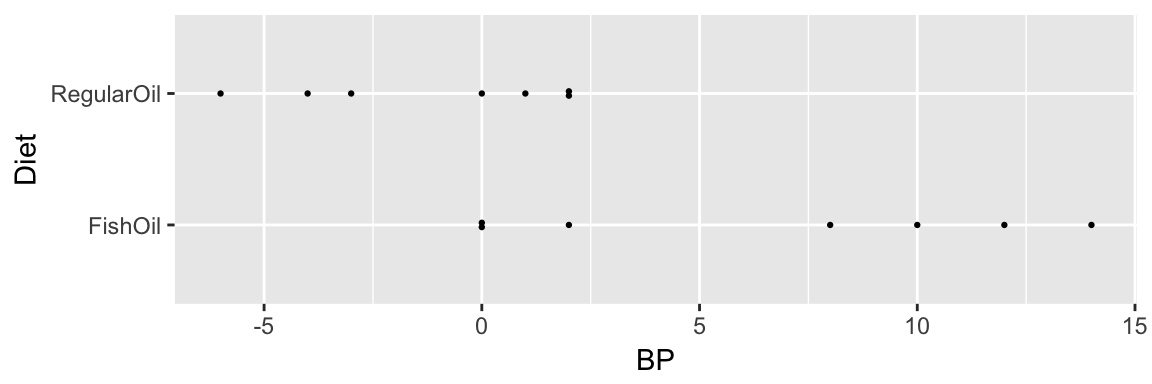
library(Sleuth3)
?ex0112

Researchers used 7 red and 7 black playing cards to randomly assign 14 volunteer males with high blood pressure to one of two diets for four weeks: a fish oil diet and a standard oil diet. These data are the reductions in diastolic blood pressure.

Example

Did the fish oil decrease BP more than the Regular Oil?

FishOil RegularOil FishOil - RegularOil
6.571 -1.143 7.714

Randomization Distribution

The randomization distirbution is the distribution of the statistic over all possible assignments of the treatments to the experimental units.

Just like the sampling distribution you can:

  • derive it
  • approximate it
  • simulate it

Simulating the Randomization Distribution

The usual null hypothesis in randomized experiments: no difference between treatments.

We observe pairs \((Y_i, T_i)\) where \(Y_i\) is observed response, and \(T_i\) is the treatment applied (let’s say \(T_i = 1 \text{ or } 2\)).

Often an additive model is assumed:

\(Y_i \, | \, (T_i = 2) = Y_i \, | \, (T_i = 1) + \delta\)

Under null \(\delta = 0\), or if null is true, we observe \(Y_i = y_i\) regardless of the treatment unit \(i\) receives.

We only observe one of \((Y_i, T_i = 1)\) or \((Y_i, T_i = 2)\), but if the null is true, we know what we would observe for person \(i\) under the other treatment, the same value.

Example cont.

Null hypothesis: no difference between treatments

BP Diet
8 FishOil
12 FishOil
10 FishOil
14 FishOil
2 FishOil
0 FishOil
0 FishOil
-6 RegularOil
0 RegularOil
1 RegularOil
2 RegularOil
-3 RegularOil
-4 RegularOil
2 RegularOil

Example cont.

Null hypothesis: no difference between treatments

BP Diet random_1 random_2
8 FishOil RegularOil FishOil
12 FishOil RegularOil FishOil
10 FishOil RegularOil RegularOil
14 FishOil RegularOil FishOil
2 FishOil RegularOil RegularOil
0 FishOil RegularOil RegularOil
0 FishOil FishOil RegularOil
-6 RegularOil RegularOil FishOil
0 RegularOil FishOil RegularOil
1 RegularOil FishOil RegularOil
2 RegularOil FishOil FishOil
-3 RegularOil FishOil FishOil
-4 RegularOil FishOil RegularOil
2 RegularOil FishOil FishOil 
## [1] -6.000000  2.857143

Many permutations

## [1] 0.007

Randomization test

  1. Pick a test statistic

  2. Simulate the randomization distribution of the test statistic under all (or many) different assignments of the treatments

    Repeat many times:

    1. Permuate treatment labels over observed values
    2. Recalculate test statistic

  3. Compare the observed test statistic to the randomization distribution

Randomization test: Comments

Exact? Consistent? Depends on the test statistic.

E.g. the test statistic ‘difference in sample medians’ isn’t an exact test for equality of population medians unless we add an additive effect assumption.

Why? Reference distribution is calculated under the asssumption that the values from the two groups are exchangable.

Sometimes used with random sampling studies (often referred to as a permutation test). Pretends population membership is like a random assignment.

The bigger picture